Importance of Aggregation before Regression Models

Recently I came across a scenario where we had to feed the data to the multi-regression model. The data had multiple granular levels to aggregate and run the model. The scenario is around the level of granularity and what happens if the data granularity identifier column is not included in the model. I am using a toy dataset to do this analysis.

• Unaggregated Dataset:

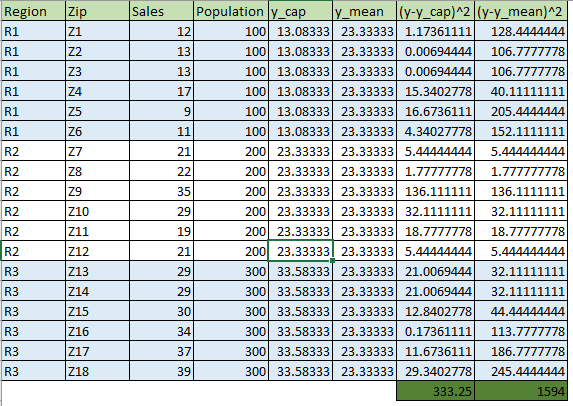
• Aggregated Dataset:

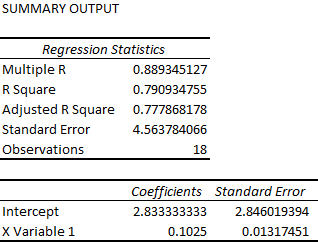
We have sales available for each zip, regions, and population for each region. I used ‘Sales’ as a dependent variable and ‘Population’ as an independent variable. When I used the data at the zip level without zip identifier, we get below summary output:

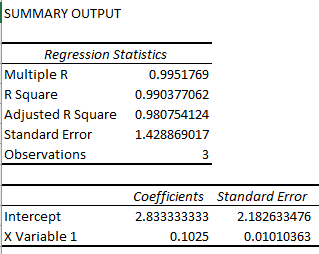
The same analysis was done on the data aggregated at the region level. The sales column represents the average sales per region. I used the same variable combinations as the input and the output variables. The summary output is below:

Key Highlights:

1. The line coefficients are the same for both the cases.
2. The aggregated data at the regional level gives a summary output with higher R Square and Adjusted R Square values, while the same dataset at zip level gives lower values of R and Adj. R Square values.
3. The standard errors of intercept and population coefficients are lower in the case of aggregated data.

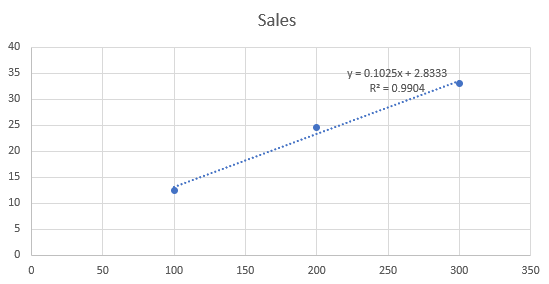
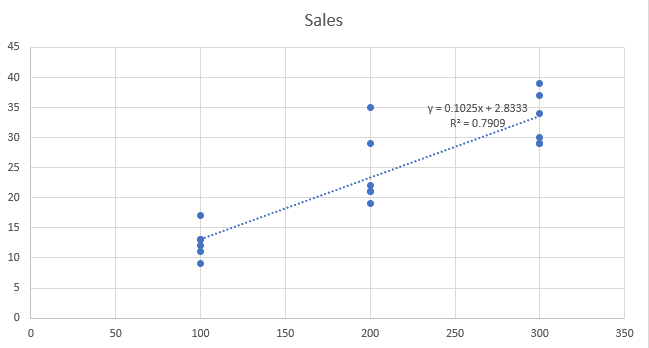
When we use the dataset at an unaggregated level, we have more points to explain the variability in the output, but it also increases the unexplained variation because of the square term. As we can see, the increase in the unexplained variation is high compared to the increase in the total variation. It makes the R Square value based on the unaggregated dataset lower than that based on the regional level data.

Also, when we use the zip level data without the zip identifier for the prediction purpose, the output will be at the aggregated level and it will be tied back to each zip. It would not give any additional information (prediction) at the zip level. So, it becomes important to use an identifier of the available aggregated data as an independent variable.

Thank you for reading.