Will Vedic maths improve existing ML Algorithms?

Hi All,

Vedic Mathematics is a collection of Techniques/Sutras to solve mathematical arithmetics in an easy and faster way. There is a famous book called Vedic Mathematics by Bharati Krishna Tirtha. It has many mathematical techniques. Though the claimed source of Vedas is rejected, the tricks of fast calculations are still intriguing.

I still remember the hot summer holidays between the school terms when I used to spend time in cricket camps, painting, or reading. I was and yet am fascinated by the Vedic mathematics tricks. I remember spending time in the Cyber Cafes (nostalgia!!) watching the math tricks on the internet and writing them down.

An idea behind writing this blog is to share my eureka moment when I accidentally stumbled upon the multiplication short-cut technique. I later discovered that the technique has some name in Vedic maths.😞

Consider an example of 2 X 2 multiplication (Don’t look for back print on the paper. Reusing the paper that comes in the mail). We use the standard way of multiplication (taught in the school) using the carry method. Multiplying by one digit, writing it down, putting 0 below rightmost digit, multiplying by the second digit, adding the carry to the result, summing up the numbers.

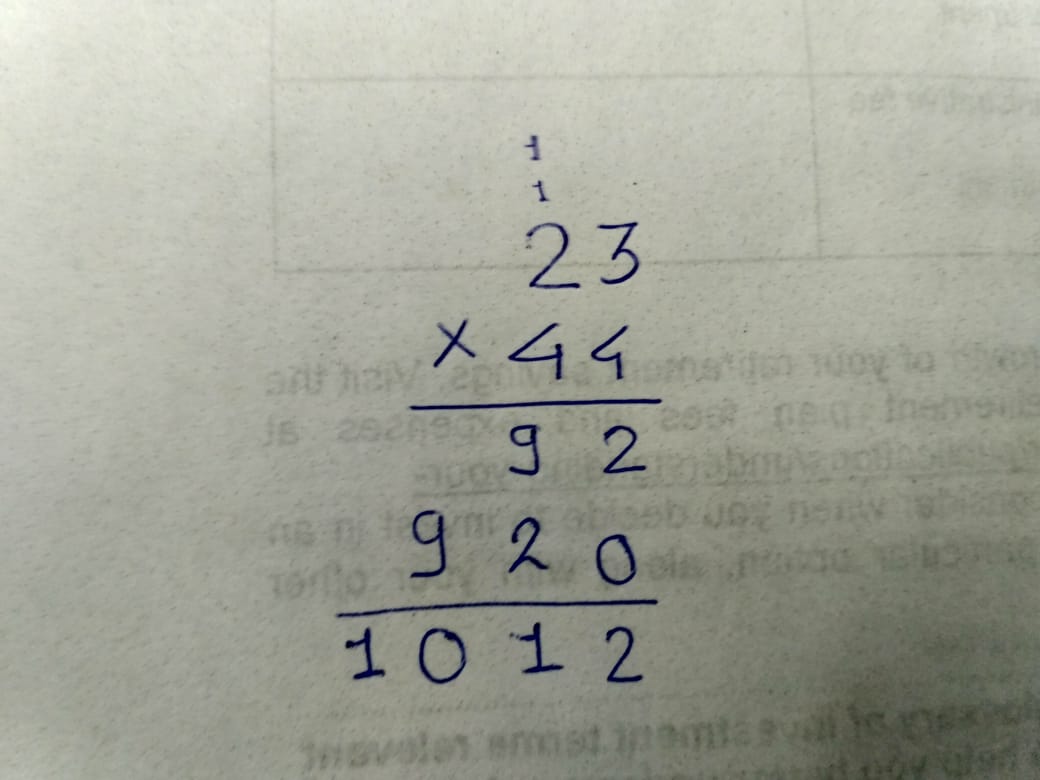
As I knew the answer, I had to play and figure out all the possible combinations which could lead to this answer. After a lot of trial and error, I could get something like this.

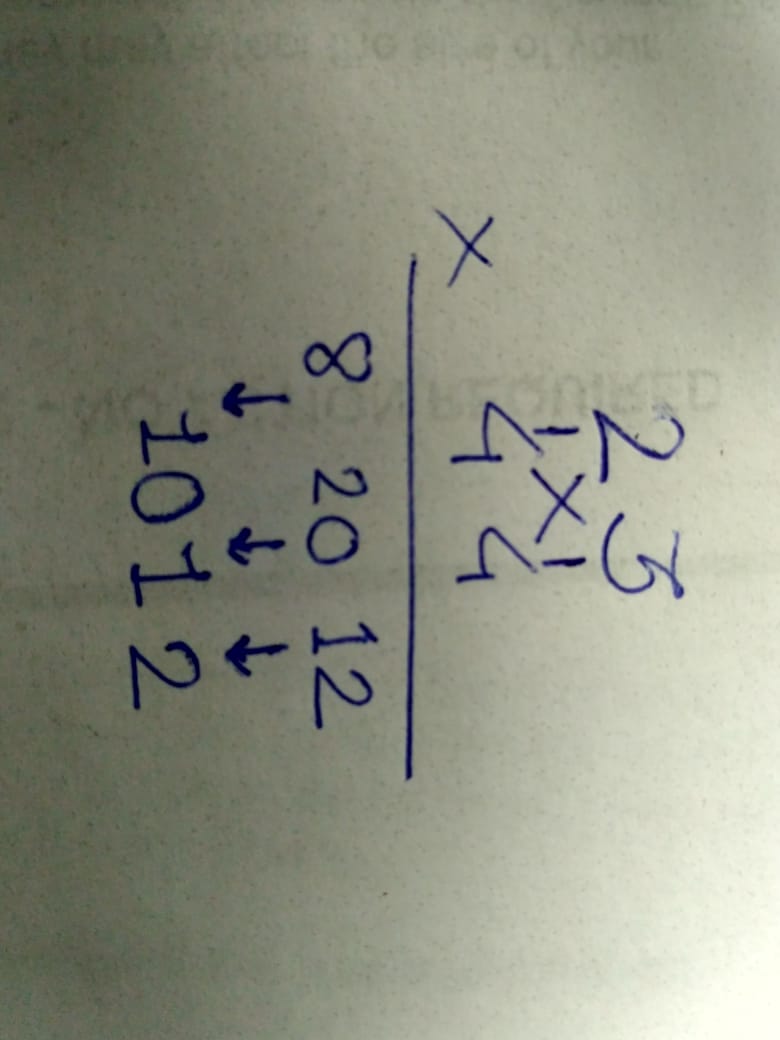
Let us understand the calculations:

1. Multiply the unit digit numbers (3 X 4 =12), write it down.
2. Multiply the cross numbers (2 X 4 and 3 X 4) and add them up (20), write it down.
3. Multiply the digits at 10’s place (2 X 4 = 8), write it down.
4. IMP STEP: if the numbers from the above steps are two-digit numbers, put the unit digit number starting from the right (2 from 12), add the 10’s place digit to the next number as a carry (1 is added to 20 and became 21). Repeat the process until the left end. DONE!!

We have to do repetitive multiplication and then chain addition. An important point that I want to highlight is the PATTERN. Once I arrived at this answer, I tried for 3 digit multiplication. The pattern was symmetric.

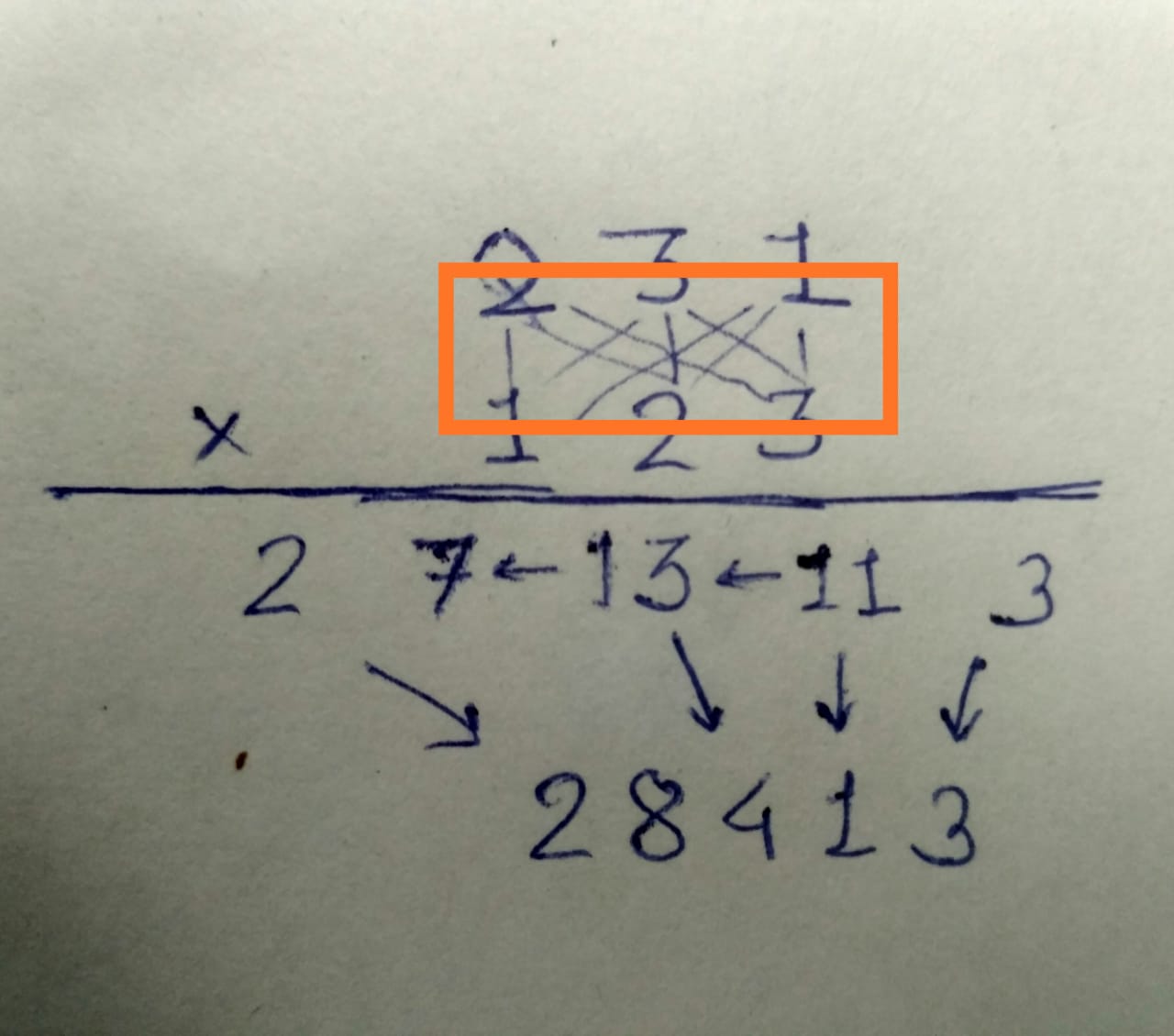
Finally, an interesting part is the multiplication pattern. It is symmetric along Y-axis. We can expand the pattern for big numbers’ multiplication. Once I started using this multiplication method, returning to the conventional one is hard. I always use it when I have to multiply.

Hope you like this technique of multiplication. I will share a couple of more techniques for readers. Practice will make it better.

Thank you! Keep returning..